2020年12月16日，中国科学技术大学管理学院王学钦教授团队与美国耶鲁大学公共卫生学院的Heping Zhang教授合作在美国科学院院刊《PNAS》在线发表题为“A polynomial algorithm for best subset selection problem”的研究论文， 针对线性回归模型的基准问题——最优子集选取，提出了一种快速算法。

发现事物间的关系是大部分科学研究的目的，这在统计学中称之为回归分析。其中，线性回归模型由于其简洁性和可解释性而成为最有用的科学研究工具之一。尽管线性回归模型被如此广泛的使用，但其中一个很基本的问题：如何在一组变量中选择最优的子模型，尚未解决。这个问题的求解被认为是NP-hard问题。得益于现代科技的发展，数据的收集变得越来越便利，在典型的生物医学研究中会收集到上百个变量，常规的全基因组研究中则涉及到成千上万甚至是百万级别的遗传变异。现有的算法难以在上万级别的实际问题中寻找到最优子集。

为了解决这个问题，王学钦团队利用排序和剪接的思想结合一个新的信息准则发展出一种新的算法，使得算法在有限步内就能得到稳定解；并证明了在一定条件下，依大概率，该算法具有多项式的时间复杂度，而且能够选出最优子集。

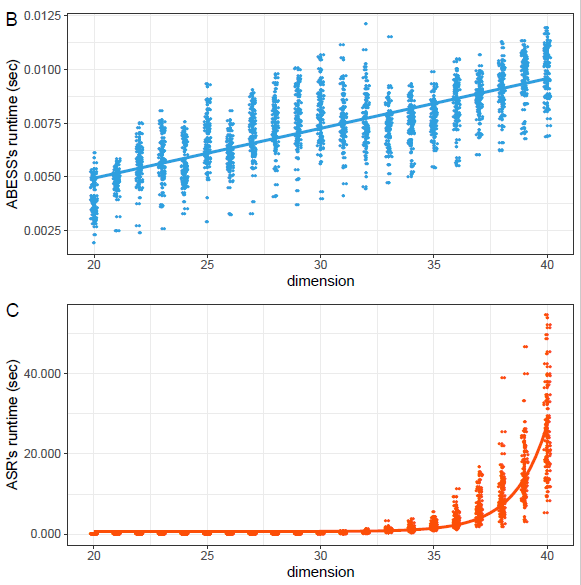
图一 算法的计算时间随着变量个数增加的散点图。其中上图是新提出的算法，下图是经典的最优子集选取算法。

中国科学技术大学王学钦教授和耶鲁大学Heping Zhang教授为论文的共同通讯作者，中山大学博士生朱俊贤和中国科学技术大学温灿红特任副研究员为论文的共同第一作者。该研究得到了国家重点研发项目，国家自然基金委项目和安徽省自然基金委项目等资助。

论文链接：https://doi.org/10.1073/pnas.2014241117